Tesla coil, oscillating electric field and capacitive coupling (electrostatic induction).
This video shows some interesting experiments with oscillating electric field.
Video also shows the basic principles of power transmission using capacitive coupling.
Device is similar to the configuration – capacitive unipolar coupling :
https://en.wikipedia.org/wiki/Wireless_power_transfer#Capacitive_coupling
Additionally, you can see:
http://iopscience.iop.org/article/10.1088/1757-899X/44/1/012007/pdf
or:
https://www.google.ch/patents/US20090206675
1. Oscillating electric field.
High voltage, which generates a Tesla coil, also generates a strong oscillating electric field.
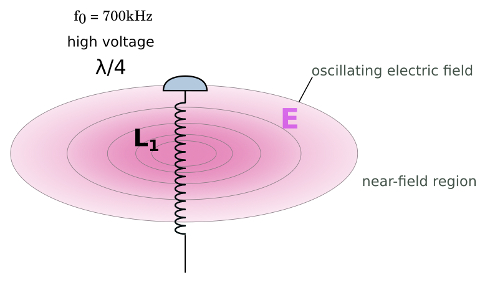
wireles power transmission – oscillating electric field
2. Inductive or capacitive coupling ?
The strong electric field enables a strong capacitive coupling and higher power transmission. Inductive coupling is negligible.
In both cases (a, b) bulb glows with the same intensity, no significant differences.
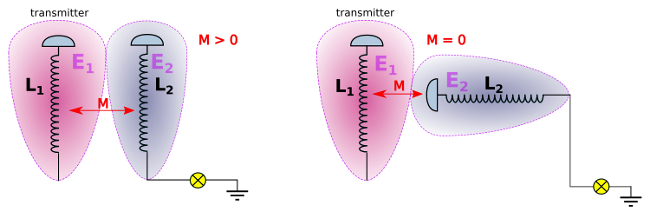
Inductive or capacitive coupling – wireles power transmission – oscillating electric field
3. Capacitive coupling (electrostatic induction) and electric dipol
a) The bulb does not light up – potential V1 = V2. b) The bulb does light up – potential V1 > V2.
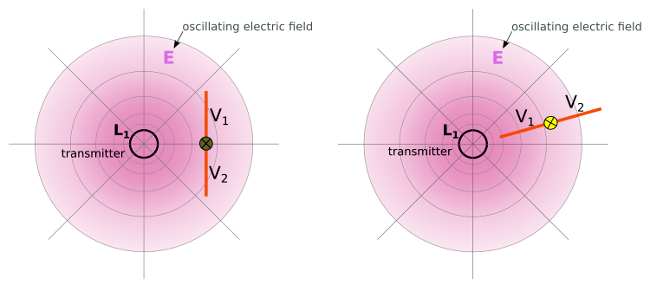
Capacitive coupling (electrostatic induction) and electric dipol – wireless power
4. Resonant capacitive coupling – dipole configuration with two coils in resonance
a) The bulb does not light up
– coils L2 and L3 are at the same distance from the coil L1
– potential V1 = V2
b) The bulb does light up
– coils L2 and L3 are at the different distance from the coil L1
– potential V1 > V2
a) b)
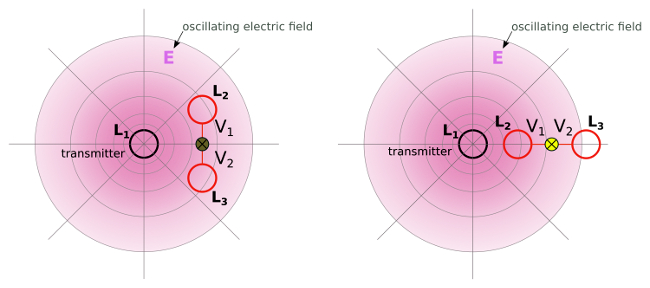
Resonant capacitive coupling – dipole configuration with two coils in resonance – wireless power – 3CT
5. By increasing the distance between the coils L2 and L3, the potential difference V1 and V2 is increased
a) The distance (l) between L2 and L3 is small
– the potential difference V1 – V2 is small
– bulb burns less brightly
b) The distance (l) between L2 and L3 is greater
– the potential difference V1 – V2 is higher
– bulb burns brighter
a) b)
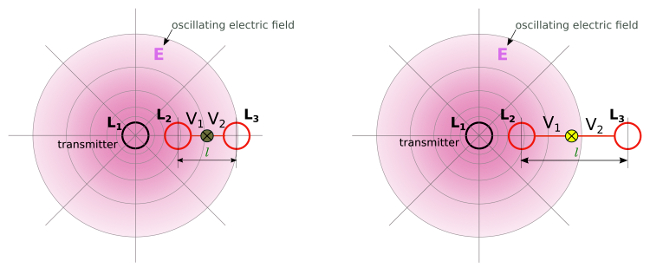
Resonant capacitive coupling – dipole configuration with two coils in resonance – wireless power – 3CT
